TPE SUR LA HOULE

3) La propagation :

1

a) Le vieillissement (ou voyage) :

 

Nous avons vu précédemment que les vagues, qui naissent et grandissent sous l'action du vent, n’ont plus besoin de lui, quand elles ont atteint ce que l'on appelle la maturité.

 

La houle va donc continuer son voyage à travers l’océan, elle se propage horizontalement, sous la forme d’une onde longitudinale, et est alors comparable à un mouvement pur, qui serait infini et ne perdrait pas d’énergie si rien ne l’altérait.

 

Les équations complètes de propagation de la houle, et plus généralement des vagues, établies par Navier Stokes sont bien trop compliquées et complexes pour de simples élèves de première S comme nous. Elles prennent en compte l'incompressibilité de l'air et de l'eau, les conservations de quantités de mouvement sous l'action des forces de pression, de gravité, de viscosité et de tension de surface.

 

N’étant pas en mesure de les démontrer et de les expliquer, nous tâcherons donc d’examiner l’ évolution de la houle après sa maturité, afin d’expliquer son mécanisme. L’image ci-dessous représente la houle dès qu’elle a atteint sa maturité :

 

 

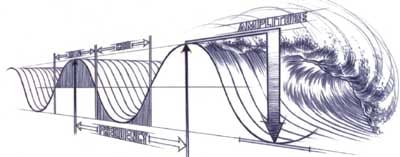
Au fur et à mesure qu’elle s’éloigne de la zone où elle a était créée, l’action de la gravité sur la houle va favoriser son étalement. Sa structure s’en voit ainsi modifiée, on observe une augmentation de la longueur d'onde et de la période, ce qui va entraîner une diminution de la hauteur et donc un étirement de la surface de l’eau : c’est ce que l’on appelle la dispersion circonférentielle. Plus une houle voyage, plus elle s’étale et à chaque fois qu’elle double, sa hauteur de réduit d’environ un tiers.

 

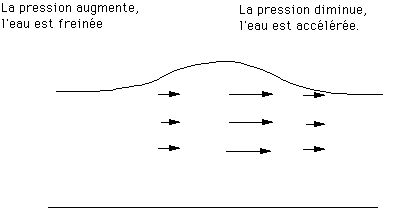
Grâce à ce phénomène, à un instant t (représenté ci-dessous), la vague s’amincit là où la vitesse des particules d’eau augmente, et la vague est étirée. En revanche, là ou la vitesse diminue, il y a augmentation du niveau, car par conservation du débit, le ralentissement des particules d’eau va « soulever » la surface de l’eau et l’on va observer l’apparition d’une bosse qui va se déplacer (ici vers la droite) :

 

Au 18^ème siècle, le physicien Daniel Bernoulli, dont les recherches traitées de la mécanique des fluides, a énoncé le principe suivant : dans un fluide en écoulement, la vitesse et la pression varient en sens inverse. Ceci peut être mis en rapport avec la variation des vitesses et des pressions dans le cas d’une vague.

En effet, la bosse s'étant ensuite déplacée, la pression est maximale à son sommet et décroît en descendant à droite. La pression décroît, donc la vitesse augmente. En revanche dans la partie gauche, la pression croît de gauche à droite (jusqu'au sommet) et la vitesse diminue:

 Les bosses ainsi créés vont permettre la progression de la houle à travers l’océan.                Les schémas ci-dessous nous montrent sa propagation, respectivement à 14 jours et à 18 jours, où chaque jour correspond à une couleur :

  

 Sur ces 2 cartes et notamment sur la deuxième, on observe très nettement les ombres causées par les différents groupes d’îles tels que Hawaï ou la Polynésie Française. C’est dans la troisième partie de notre TPE que nous expliquerons comment se comporte la houle en présence de rivages ou de côtes…

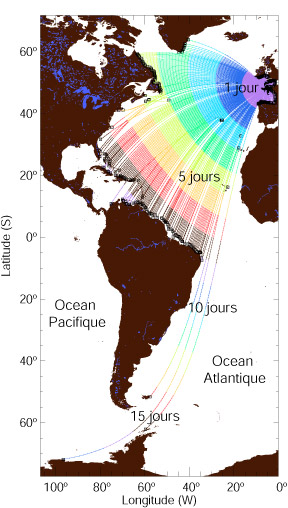
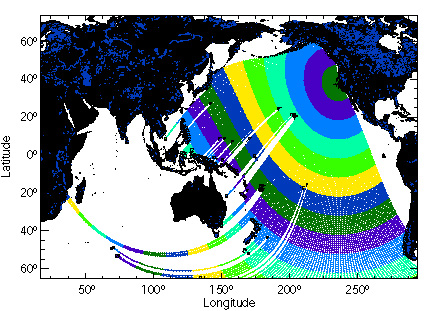
 A noter également qu’il n’est pas rare que plusieurs trains de houle générés dans des zones différentes, se combinent. Ce phénomène sera d’autant plus fréquent que la houle vient de loin. Elle peut aussi se superposer à une mer locale, plus courte et généralement de direction différente, on parle alors de mers croisées.

b) La célérité (ou vitesse de propagation) :

            La célérité correspond à la vitesse de propagation une crête ou d’un creux d'une vague.

La célérité de la vague croit avec son amplitude et elle est différente selon le type d'onde.

Or, dans la première partie nous avons précisé que la houle était une onde courte, la célérité de la houle est donnée par l’expression c = λ  / T

 

Cette formule correspond à un rapport faisant intervenir au numérateur, la longueur d’onde λ et au dénominateur, la période T de la houle.

 

On peut donc en déduire que l’onde ayant la longueur d'onde la plus grande se propagera le plus rapidement. C'est d'ailleurs grâce à cela que la houle s'organise pour devenir plus propre, c'est ce que l'on appelle la dispersion radiale. En effet, les longueurs d'onde les plus longues, donc les plus rapides, distancent les longueurs d'onde les plus courtes qui sont  plus lentes.

Par ailleurs, voici un tableau montrant la relation qu’il existe entre l'éloignement d'une perturbation, la hauteur de la houle, sa période et le temps qu'il lui faut pour arriver et déferler sur nos plages :

 

1

Le tableau ci-dessous donne lui une idée de l'ampleur de la transformation de la vague à travers l'évolution de sa période, de sa longueur et de sa célérité :

1

Ce tableau nous permet de bien nous rendre compte que plus la période et la longueur d'onde sont importantes, plus la houle va vite.

1

c) Le mouvement des particules d’eau :

1

Comme nous l’avons dit précédemment, le voyage de la houle se fait par transport d’énergie et non de matière. Au passage de l’onde, les particules d’eau sont misent en mouvement  mais restent pratiquement à la même position.

 

Pour allez plus loin dans ces explications, nous allons développer la théorie d’Airy, un célèbre physicien anglais du 19^ème siècle.

 

Ce dernier à démontrer que le mouvement des particules d’eau est une oscillation périodique, dont la vitesse varie en fonction de la profondeur de l’océan. Sous l’effet de cette propagation, la crête de la vague va s’avancer, et le mouvement des molécules d’eau va se faire sous forme d’orbites circulaires. Ceci va engendrer un faible mouvement d’avancée, un peu plus fort que le mouvement de retrait, afin que les particules ne se retrouvent pas exactement, mais quasiment à leur position initiale.

 

Ainsi, dans leur mouvement, les vagues font tourner sur place les particules voisines de la surface, qui forment alors des orbites circulaires dont le diamètre est égal à la hauteur de la vague.

Vous trouverez ci-dessous un schémas nous montrant ce phénomène, chaque orbite circulaire étant numérotée, vous pourrez observer le déplacement par rotation, des particules d’eau qui la composent, avec un écart de un huitième de période entre les 2 « prises »   :

 

 

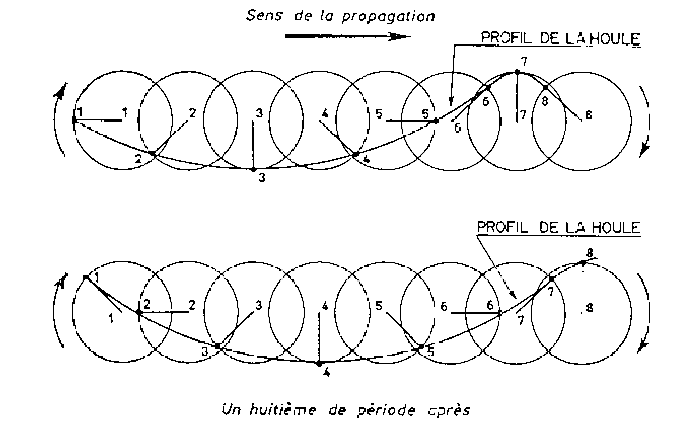
Une petite animation pour y voir encore plus clair…

 

 

Ce mouvement se poursuit sous l’eau mais avec une amplitude moindre puisque celle- ci diminue avec la profondeur. C’est pourquoi, une profondeur égale à une demi-longueur d’onde de la vague, le diamètre des orbites, décrites par les particules d’eau, est 25 fois plus petit qu’à la surface.

1

Ce phénomène va aller en s’accentuant, d’autant plus que la profondeur sera importante. En effet, la masse d’eau présente au-dessus d’une molécule se trouvant très en profondeur, va peser sur celle-ci, limitant de ce fait ses mouvements . De plus, la colonne d’eau aura une certaine hauteur, correspondant à la profondeur de la particule, et aura un poids très important. Le cercle décrivant la trajectoire de la molécule aura donc un diamètre plus petit que celui décrivant la trajectoire d’une particule plus proche de la surface :

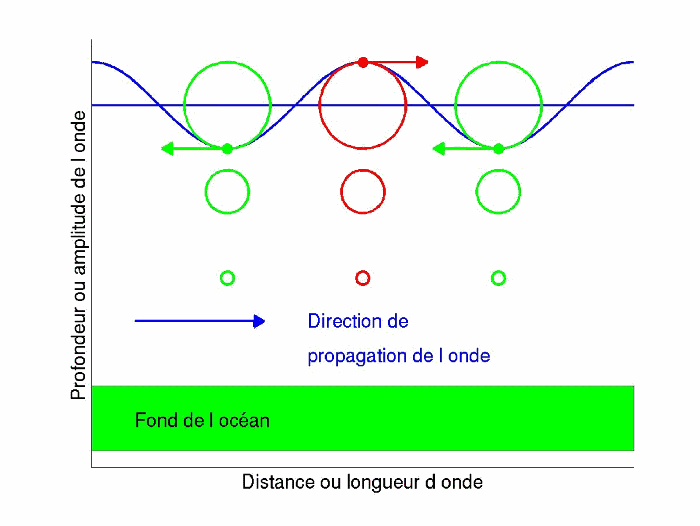
            A noter qu’une formule existe pour calculer le diamètre des cercles décrivant les trajectoires des particules d’eau, celle-ci, qui met en relation l’amplitude, la longueur d’onde et la profondeur, est bien trop compliquée pour que nous la démontrions.

 

Il est néanmoins très important de préciser qu’habituellement, un point atteint par une onde, reproduit l’état de la source avec une amplitude moindre et un retard dû à la durée nécessaire à l’onde, pour parcourir la distance qui sépare la source de ce point.

C’est ce qui nous est montré par cette animation, où le point M effectue le même mouvement que la source, c'est à dire un mouvement vertical :

Vous aurez donc compris que ce n’est pas le cas et que c’est bien plus complexe s’agissant de la houle.

 

Dessin combinant les deux aspects de la Théorie de Airy !

 

 

S’agissant de l’énergie mécanique (E) de la houle, composée d’énergie potentielle et d’énergie cinétique. Nous décidé de ne pas développer sa formule car cela n’est pas nécessaire pour expliquer la propagation de la houle, même si celle-ci se fait par transport d’énergie.

 

Par ailleurs, lorsque les vagues s’approchent du rivage le mouvement des particules d’eau est modifié. Nous allons y revenir dans la troisième partie de notre TPE, ci-après…