DEVELOPPEMENT (PARTIE 1)
1) Qu'est-ce que la houle ?
a) Définition :
La houle est un mouvement ondulatoire de la surface de la mer, c’est une suite infinie d’ondulations parallèles presque identiques, qui se propagent de façon sensiblement uniforme vers le rivage.
C’est un type de vagues forcées par le vent, qui se propage en dehors de sa zone de génération (ceci sera expliqué dans la partie « formation de la houle »).
D’un point de vue plus physique, la houle correspond à une onde progressive mécanique périodique sinusoïdale.
Les ondes progressives mécaniques périodiques sont le phénomène qui accompagne la propagation, dans un milieu matériel supposé linéaire et illimité, d'une perturbation se répétant indéfiniment. Elles correspondent à des déformations périodiques d'une interface.
Elles sont dites sinusoïdales si la perturbation créée par la source, est une fonction sinusoïdale du temps, de période T.
La houle se propage donc de façon périodique à la surface de contact entre l'eau et l'air, par vibration de matière. Il s'agit d’un déplacement d'énergie et non de matière.
D'autre part, la houle est une onde longitudinale. En effet, il s’agit d’une perturbation se propageant dans un milieu, sans transport de matière, et de plus, la déformation du milieu, et la direction de propagation de l'onde ont la même direction.
En océanographie, les ondes de surface se matérialisent par une déformation de la surface de la mer, c'est-à-dire une déformation de l'interface entre l'atmosphère et l'océan.
Par ailleurs, la houle est ce que l'on appelle une onde courte (nous expliquerons pourquoi et quelles en sont les conséquences dans la suite notre TPE).
Bien qu'en réalité, la houle ne soit pas un phénomène périodique qui s'interprète en fait comme une somme d'une infinité de composantes sinusoïdales infiniment petites, nous considèrerons sa représentation comme une simple et parfaite sinusoïde, dans le but de pouvoir l’étudier et vous expliquer son mécanisme sous un aspect physico-mathématiques.
b) Caractéristiques physiques :
Une onde, et donc la houle se caractérise par :
Sa période notée T : c’est l'intervalle de temps (en secondes) qui s'écoule entre le passage de deux crêtes successives au niveau d'un point fixe.
Sa fréquence notée f : c'est le nombre de trains de houle (en Hertz) passant en un point fixe en une seconde, elle est égale à 1 / T.
Sa longueur d'onde notée λ ou L : c'est la distance (en mètres) entre deux crêtes ou de creux de deux vagues successives.
Sa hauteur notée H : c'est la dénivellation verticale (en mètres) entre la crête et le creux de la vague.
Son amplitude notée A : c’est la dénivellation verticale (en mètres) entre la crête de la vague et le niveau de la mer au repos, soit une demie hauteur.
Sa célérité ou vitesse de propagation notée c : c'est la distance parcourue par une crête ou un creux en même temps donné (en mètres par secondes), elle est égale à λ / T, (nous développerons plus en détails cette formule dans la partie « propagation de la houle »).
Sa cambrure notée C : c’est le rapport entre la hauteur et la longueur d'onde, elle est égale à H/ λ, (nous utiliserons cette formule dans la partie « déferlement de la houle »).
Son Fetch : c'est la distance sur laquelle le vent souffle pour engendrer la houle, (nous expliquerons plus précisément son importance dans la partie consacrée à la « formation de la houle »).
Sa profondeur notée D : c’est la distance (en mètre) entre la ligne de repos et le fond de l’océan (elle aura son importance dans la partie concernant le « déferlement de la houle »).
Voici un schéma pour y voir plus clair…
c) Etude de la fonction sinus :
La houle se modélisant par une sinusoïde nous allons étudier la fonction sinus :
1) Ensemble de définition :
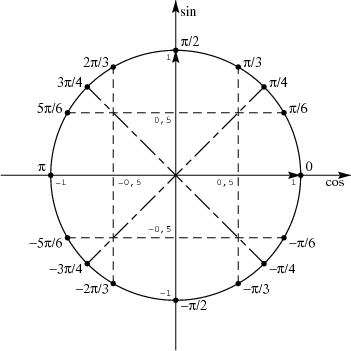
Pour tout point M d'un cercle, on peut associer une ordonnée appelée y = sin(x) où x correspond à l'angle MÔI exprimé en radians. La fonction sinus est donc définie sur R.
f (x) = sin(x) définie sur R.
2) Parité et périodicité :
La fonction sinus est impaire car sa courbe est symétrique par rapport à l’origine, de plus sur le cercle trigonométrique sin (-x) = -sin(x)
Ex : -sin(π) = sin(-π) = 0
m
Ce qui permet de restreindre l'étude à la partie de [-π ;π ]. La fonction sera donc étudiée sur l'intervalle [0 ; π].
La fonction sinus est périodique sur 2π : sin (x + 2π) = sin(x)
L’axe de symétrie est l’origine du repère, le point O.
3) Dérivabilité :
On sait que la fonction sin (x) est dérivable sur R et que f’(x) = cos (x).
4) Variation :
On peut étudier la fonction sur l’intervalle [-π ; π].
De plus on sait que comme la fonction est impaire, on peut l’étudier sur [-π ; 0] et les variations sur [0 ; π] seront inversés.
f ’(x) = cos (x) donc on étudie le signe de la fonction cosinus grâce au cercle trigonométrique :
- la fonction cosinus est inférieure à 0 sur [-π ; - π/2]
- la fonction cosinus est supérieure à 0 sur [-π/2 ; 0].
|
x |
-π -π/2 |
0 |
|
f ’(x) |
- |
+ |
|
f (x) |
|
|
|
x |
-π -π/2 |
0 |
π/2 |
π |
|
f ’(x) |
- |
+ |
+ |
- |
|
f (x) |
|
|
|
|
5) Extremums :
1
- Maximum : y = 1 en x = π/2
- Minimum : y = -1 en x = - π/2
Tous droits réservés - Créer un site avec OnLC.fr